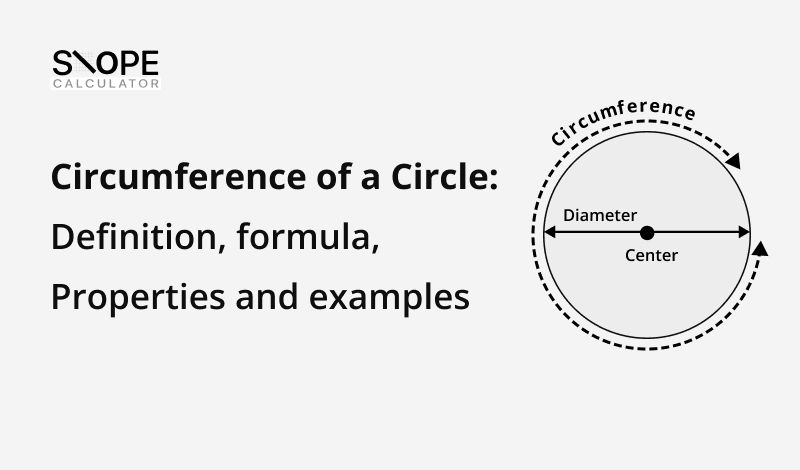
The circumference of a circle gives the length of the outer border of a circular shape. It is similar to the perimeter of any other two-dimensional figure. The term perimeter is specifically referred to as circumference in the case of a circle.
The circumference is an important measurement since it is directly related to the size of any circle. It is essential for anyone studying geometry or any field that involves circular objects.
In this blog, we will discuss the definition of the circumference with an explanation. We will explain both the mathematical formula and properties of the circumference. We will include examples for our readers in the example section to clarify this concept.
The circumference of a circle is the distance of its outside boundary. It measures the entire length of the border of the circle. Let's learn this concept through real-life examples. Imagine a girl running around a circular park and completing a single rotation.
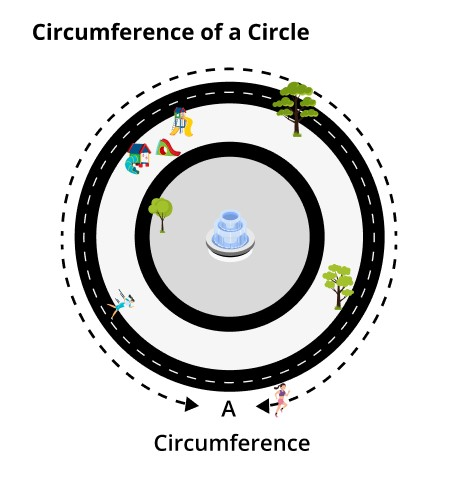
The distance covered by her in this circular track in one trip is called the circumference of the park.
The circumference of a circle is a basic concept in geometry. We can apply it in our daily life to compute the perimeter of a circular racetrack, determine the belt length required to encircle a pulley or calculate the distance traveled by a wheel during one complete round.
The circumference of a circle can be defined as the length of the boundary that encloses a 2D circular shape. If we cut a circle and create a straight line, the total length of this line would be the circumference of a given circle.
Circle circumferences are measured in length units such as feet, inches, centimeters, meters, miles, or kilometers. Let’s learn about a few important terms associated with circles to understand how to find the circumference of a circle.
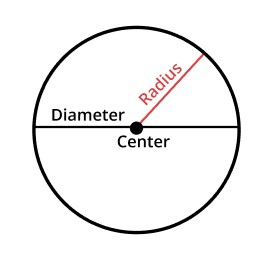
A circle is a set of all points that are a constant distance from a fixed point, known as the center of the circle.
The diameter is a straight-line segment that passes through the center of the circle and connects two points on the boundary of the circle.
The radius of a circle is the distance from the center of the circle to any point on its circumference. The radius (r) is equivalent to half of the diameter (i.e. r = d/2).
The circumference measures the overall length of the outer border of the circle. It can be evaluated using the formula:
C = 2 π r
In this formula:
3.14159 in decimal).We can also calculate the Circumference using the diameter with the following formula:
C = π d
Where:
Note that the choice of the formula depends on the given data.
The circumference has the following essential characteristics:
π = C/d).The Circumference of any 2D circular shape can be evaluated in a few simple steps:
The following examples illustrate how to calculate the circumference of a circle manually.
Example 1:
If the circle has a radius of 7 cm, find its circumference.
Solution:
Given Data:
Radius (r) = 7cm
∴ π ≈ 3.14
The circumference of a circular shape can be calculated using the following formula.
C = 2πr
Substitute these given values in the above formula, we get
C = 2 × 3.14 × 7
Circumference = 43.96 cm
Example 2:
Calculate the length of fabric required to make a 36-inch-radius round dining tablecloth.
Solution:
Here;
r = 36 inches
An estimated value of pi (π) is 3.14.
∴ C = 2πr
Substitute the given values into the formula:
Circumference = 2 (3.14) (36)
C = 226.08 inches
The tablecloth requires around 226.08 inches of fabric.
Example 3:
Calculate the circumference for the circular region with a 10-meter diameter.
Solution:
Give:
Diameter = d = 10
∴ π ≈ 3.14
The formula for the circumference when d is given:
C = πd
Put the value of d and pi in the formula of circumference.
C = 3.14 × 10 m
Circumference = 31.43 m
Thus, the circumference with a radius of 10m is approximately 31.43m.
To solve problems of calculating the circumference of a circle, Use our circumference calculator for precise results quickly.