Slope Calculator is an easy-to-use tool. You will have to
Result
\(X_1 = \) , \(Y_1 = \)
\(X_2 = \) , \(Y_2 = \)
| Point grade | Values |
| Percentage Grade | |
| Angle \(θ\) | deg |
| Distance | |
| \(Δx\) | |
| \(Δy\) | |
| Y - Intercept | |
| X - Intercept |
The slope formula calculator has great importance in both Mathematics and Physics. It helps to find the gradient (slope) of a line by taking two points or line equations as input.
In addition to finding the simple slope, it finds a whole lot of other slope and line characteristics as well. These include:
Slope in math has the same meaning as in English and that is “Steepness”. Except in maths, we use the word slope for the steepness of lines and curves.
It is also known as gradient, incline, and slant. Daily life examples of slope include roofs, slides, and steep mountains.
The slope formula is ‘rise over run’. Mathematically it can be written as:
m = (Y2 - Y1) / (X2 - X1)
m = 𝚫Y / 𝚫X
These can be any two-point of a line in a cartesian plane.
Slope can be positive, negative, zero, or undefined. The types of slope depend on their values and the sign with the value. For a quick review, a slope that has
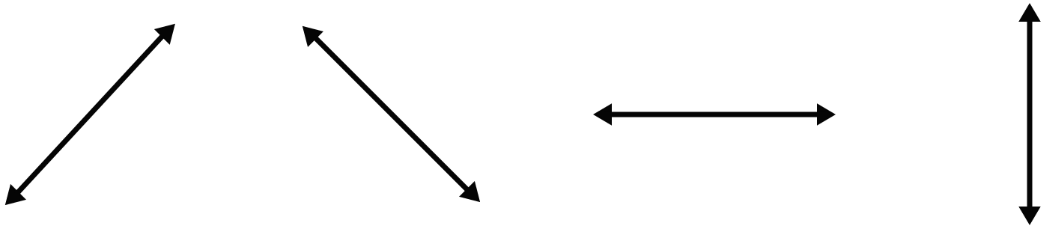
| Positive | Negative | Zero | Undefined |
| Increasing from Left to Right | Decreasing from Left to Right | Horizontal Line. Not Increasing or decreasing from Left to Right | Vertical Line. The line doesn't move to the Left or Right |
If you need to find a slope quickly and without any error, you can use the slope finder for that purpose. But if you want to calculate it yourself, keep on reading the example below.
Example:
Find the slope of the line passing through points (3,6) and (8,2).
Solution:
Step 1: Identify the values.
X1 = 3
X2 = 8
Y1 = 6
Y2 = 2
Step 2: Find the difference between the points.
𝚫X = X2 - X1
= 8 - 3
= 5
𝚫Y = Y2 - Y1
= 2 - 6
= - 4
Step 3: Solve the fraction 𝚫Y / 𝚫X.
m = 𝚫Y / 𝚫X
= -4 / 5
= -0.8
Hence the slope of the line is -0.8 and negative in nature.
Slope can also be found if you have an equation of a line. Let’s find the slope using the line equation.
Example:
Find the slope of line in the following line equation.
4y – 2x + 5 = 0
Solution:
Step 1: Arrange the equation in the form of y = mx + c
4y = 2x – 5
y = (2x – 5)/4
Step 2: Simplify the right side of the equation.
y = 2x/4 – 5/4
y = 0.5x – 1.25
Now that we have the equation of the straight line, a slope can be found by comparing it to the original equation where m represents the slope.
y = mx + c
y = 0.5x – 1.25
Slope (m) = 0.5
What is meant by the slope of a line?
The slope is the measure of the rise over run of the given coordinate points of x and y. Mathematically,
Rise over run is (y2 - y1)/(x2 - x1)
What is the symbol of the slope?
The measure of the steepness of the line is denoted by the letter "m". Such as
m = rise/run

1 year ago
1 year ago

1 year ago