
The slope intercept form is a way of representing a linear equation in a two-dimensional coordinate plane. It defines the connection between two variables x and y in a straight line. This form is most useful when the slope and y-intercept of the line are known. The equation of a straight line may also be found using the slope-intercept form if two points on the line are given.
In this blog post, we’ll discuss the definition of slope intercept form and learn how to determine the equation of the line by using it along with examples.
The slope intercept form is a particular and widely used form for writing the equation of a line. This form is highly effective in simplifying the representation and interpretation of straight-line equations. Slope intercept form requires the slope “m” and y-intercept “b” of the line to determine the equation of a line.
Assume that a line has slope m and y-intercept b. The slope-intercept form for linear equation with slope m and y-intercept b can be expressed as:
y = mx + b
Here m and b can be any real numbers. The value of m determines the inclination of a line while the value of b represents the point where the line crosses the y-axis.
Consider a straight line with slope m and intersects the y-axis at (0, b). Also (x, y) is any other arbitrary point on this line.
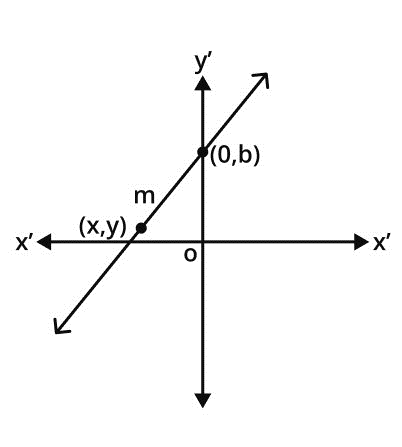
The mathematical expression for the slope of a line passing through two points (x1, y1) and (x2, y2) is as follows:
Slope = m = (y2 – y1)/(x2 – x1)
Here
Put these values in the slope formula,
m = (y – b)/(x – 0)
m = (y – b)/(x)
Multiply ‘x’ on both sides.
mx = y – b
After rearranging the above equation, we get
y = mx + b
This is the general form of slope-intercept form.
The formula for the slope-intercept form used to write the equation of a line is:
y = mx + b
Where,
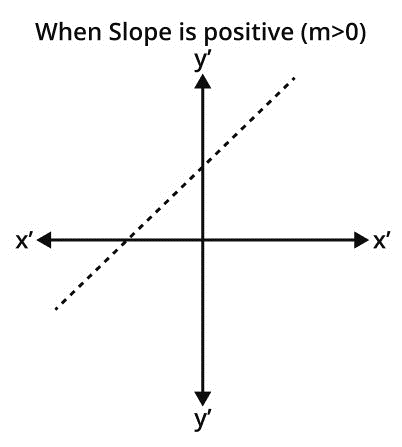
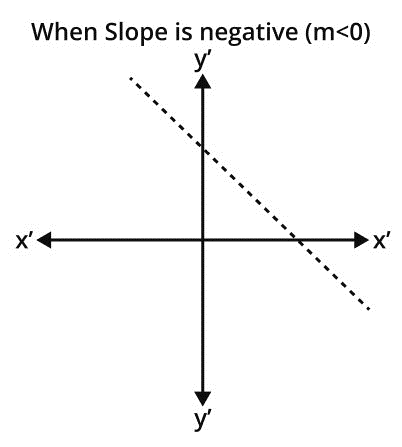
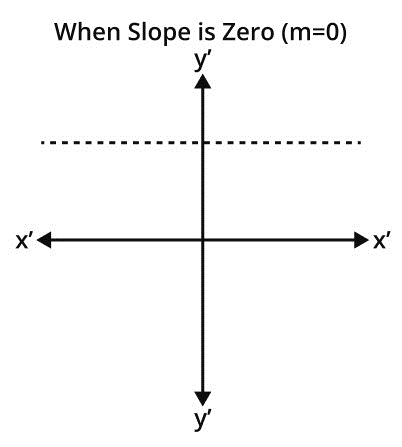
Some properties of slope intercept form are given here:
Let’s learn how to find the slope-intercept form in easy steps:
Slope = m = (y2 – y1)/(x2 – x1)
Move on to the next step if the slope is already given.
The given point and slope m can be used to find b. Substitute the values of x, y, and m into the equation (y = mx + b) and calculate it for b.
Go to the next step if it is also given in question.
y = mx + b
Here are a few examples to clarify the above steps.
Let's look at a couple of examples to see how slope intercept form works.
Example 1: (If Two Points are given)
Determine the equation of a straight line that passes through the points (2, 3) and (-1, 5).
Solution:
Here
(x₁, y₁) = (2, 3)
(x₂, y₂) = (-1, 5)
We will use the following formula to find the slope of this line.
m = (y₂ - y₁) / (x₂ - x₁)
m = (5 - 3) / (-1 - 2)
m = 2 / -3
Now that we have the slope, we can use the slope-intercept form to find b:
y = mx + b
y = (-2/3) x + b
As the line passes through the points (2, 3) we can substitute the values of x and y into the equation as follows:
3 = (-2/3) (2) + b
3 = -4/3 + b
b = 11/3
Substitute the value of b and m in the general equation of slope-intercept form.
y = (-2/3) x + 11/3
It is the equation that passes from (2, 3) and (-1, 5).
Example 2: (If Slope & y-intercept are given)
Find the equation of a straight line when the slope of a line is 3 and the y-intercept of the line is - 6.
Solution:
Here,
Slope = m = 3
Y-intercept = b = - 6
Substitute these values in the standard equation of the slope-intercept form.
∴ y = mx + b
y = (3) x + (- 6)
y = 3x – 6
Example 3: (When 1 Point and Slope are known)
Determine the equation of a line that passes from the point (2, 5) with a slope of 3.
Solution:
To find the equation of this line, we can use the slope-intercept form as follows:
y = mx + b
y = 3x + b ______ (1)
We know that the line passes from the points (2, 5), so we can substitute the values of x and y into the equation as follows:
5 = 3(2) + b
5 = 6 + b
b = -1
Put the value of b in equation (1), we get
y = 3x – 1