The point-slope form is a mathematical representation of a straight-line equation within a two-dimensional coordinate system. This form helps us to write the equation of the line using just one point and the slope of a line. A line’s equation is a linear equation where every point on a line must satisfy it.

The straight-line equation is often represented in the following form.

• Point slope form
• Intercept form
• Slope-intercept form
• Two-point form

However, we will restrict ourselves to only the point-slope form of the line in this blog post. We will cover its definition with mathematical equations and properties. We will learn how to find out the point-slope form with the help of examples.

What is the Point Slope Form of a Line?

In algebra, the point-slope form is one of the most common methods for representing the equation of the straight line. This form is more effective if we know the slope and at least one point of the line. It is a helpful method in geometry and algebra for working with lines in the Cartesian coordinate system. The equation of a straight line passes from the point (x₁, y₁) with a slope of (m) in a point-slope form is written as:

y - y₁ = m(x - x₁)

Here (x, y) is any point lying on a line.

How to Derive the Formula of Point Slope Form?

Let us learn how to find the standard equation of point slope form. We will apply the definition of slope to derive the equation of point slope form. Assume a line passes from the points (x₁, y₁) and (x, y).

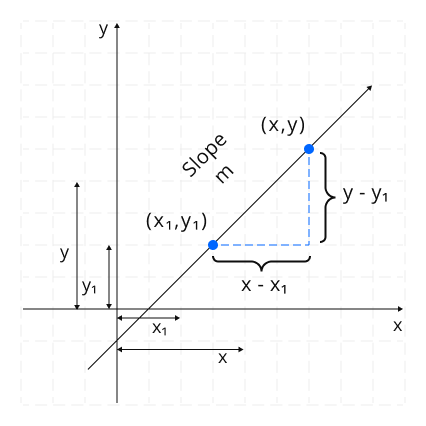
The slope of this line is the ratio of the rate of change in the y-coordinates to the rate of change in the x-axis.

 m = (y - y₁) / (x - x₁)

Multiply both sides of the above equation by (x - x₁).

m (x - x₁) = (y - y₁)

The above equation can also be written as:

y - y₁ = m(x - x₁)

That is the formula of point slope form.

Properties of Point Slope Form

Here are some characteristics of the point-slope form that enhance its importance.

• We often choose the point-slope equation when we know a specific point on the line and its slope.
• The point-slope equation represents a straight line on the XY plane and every point on the line satisfies this equation.
• It helps us to find the equation of a line in a form that is easy to interpret. We can easily look at the slope of the line and the point where it passes through.
• Point slope form can be easily converted into other forms such as slope intercept or standard form if needed.
• It can be used to graph a line quickly. We can plot the given point and then use the slope to find other points on the line.

How to Write the Equation of a Line in Point Slope Form?

Steps on how to write the equation of a straight line in point-slope form.

1. Write down the points x₁, y_1, and slope m. If the slope of a line is not given, then you have to find it first. Our slope calculator will help you to do this.
2. Use the formula of point-slope form.
3. Substitute the given values into the equation of point slope.
4. Simplify the equation to get a standard form of the linear equation.

Graphic Representation of the Point Slope Form

Follow the following steps to represent the point-slope form on the graph.

1. Identify the point of the line and locate it on the graph.
2. Use the slope to plot a second point by moving vertically and horizontally from the first point.
3. Draw a line through the points to express the equation in point-slope form on the graph.

Examples of Point Slope Form

You can try our point slope form calculator to solve the examples of point slope form quickly. However, Let's solve various examples to learn the point-slope form manually.

Example 1:

Determine the equation of a straight line that passes from the point (3, 5) with a slope of 3.

Solution:

Step 1: First, identify the points of the line and its slope.

Slope (m) = 3

x₁ = 3 and y₁ = 5

Step 2: Apply the formula of point slope form.

∴ y – y1 = m(x – x1)

Step 3: Substitute the values:

y – 5 = 3(x – 3)

Step 4: Expand and simplify:

y – 5 = 3x – 9

0 = 3x – 9 – y + 5

0 = 3x – y – 4

Thus, an equation of a line 3x – y – 4 = 0 passes through a point (3, 5) and has a slope of 3.

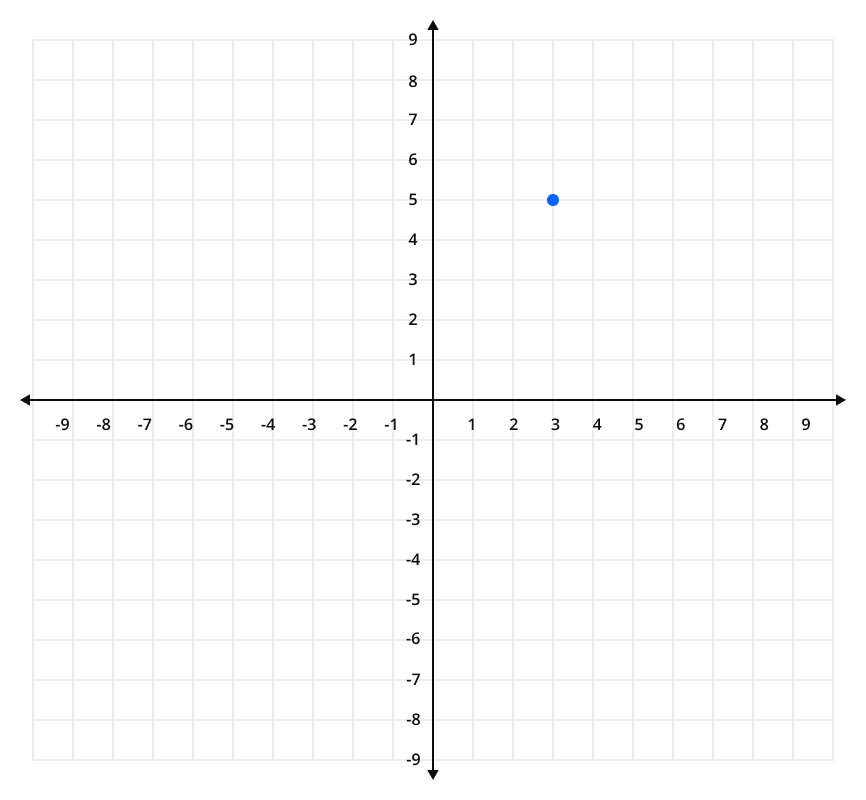
Graphing:

Step 1: Plot a point (3, 5) on the graph.

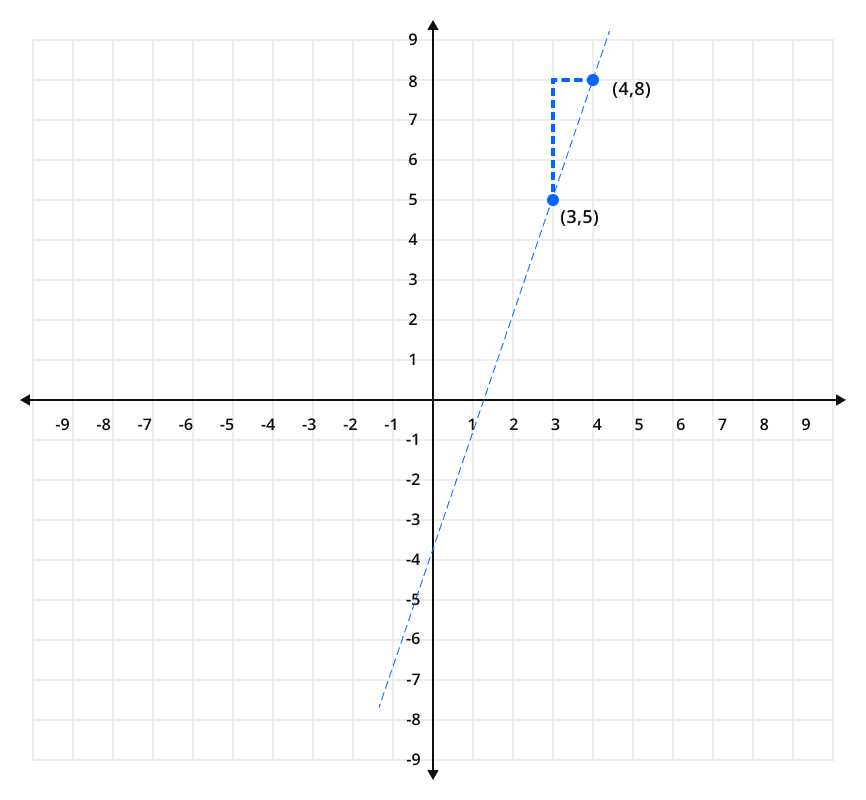
Step 2: Use the definition of slope to plot a second point.

m = 3/1

As we know that:

Slope = change in y / change in x 

Or Slope = rise/run

Rise 3 steps up and move 1 unit right from the given point (3,5) to get another point (4, 8) on the graph. Join these two points by constructing a straight line

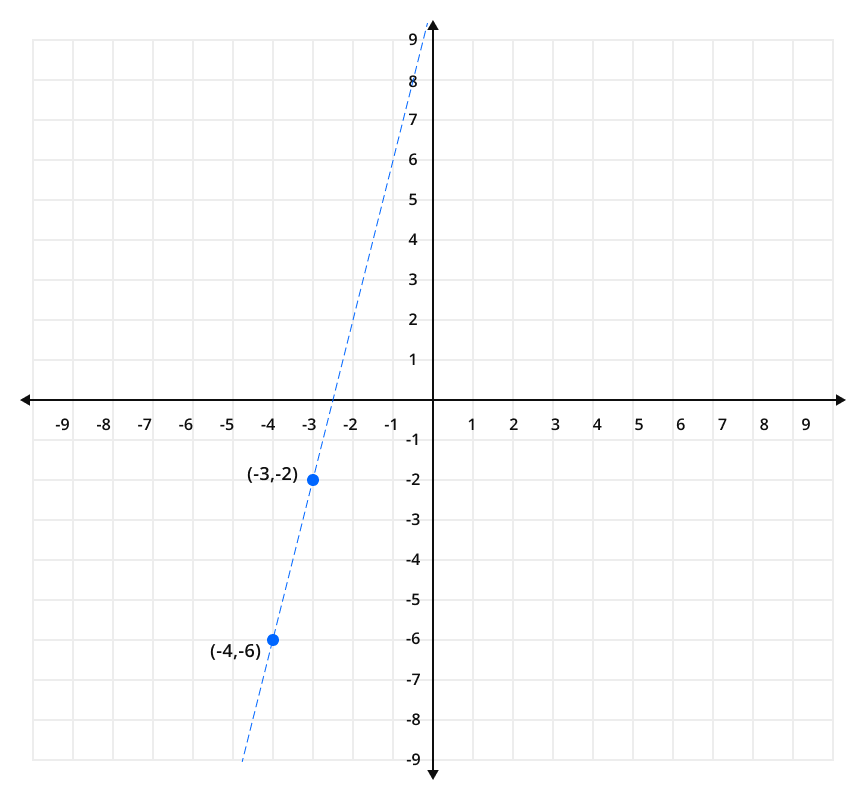
Example 2:

Find a straight-line equation that passes from the point (– 4, – 6) and has slope 4.

Solution:

Step 1: write down the given slope and points.

Slope: m = 4

Point: (x₁, y₁) = (– 4, – 6)

Step 2: Put the provided values in the point-slope form equation.

y – (– 6) = 4(x – (– 4))

y + 6 = 4(x + 4)

Simplify the above equation and Rearrange it into standard form.

y + 6 = 4x + 16

4x – y + 10 = 0

That is the required standard form of line.

Graphic Representation: